Kick Start Round E 2021
올해 들어 다섯 번째 competition인 Round E를 치렀다.
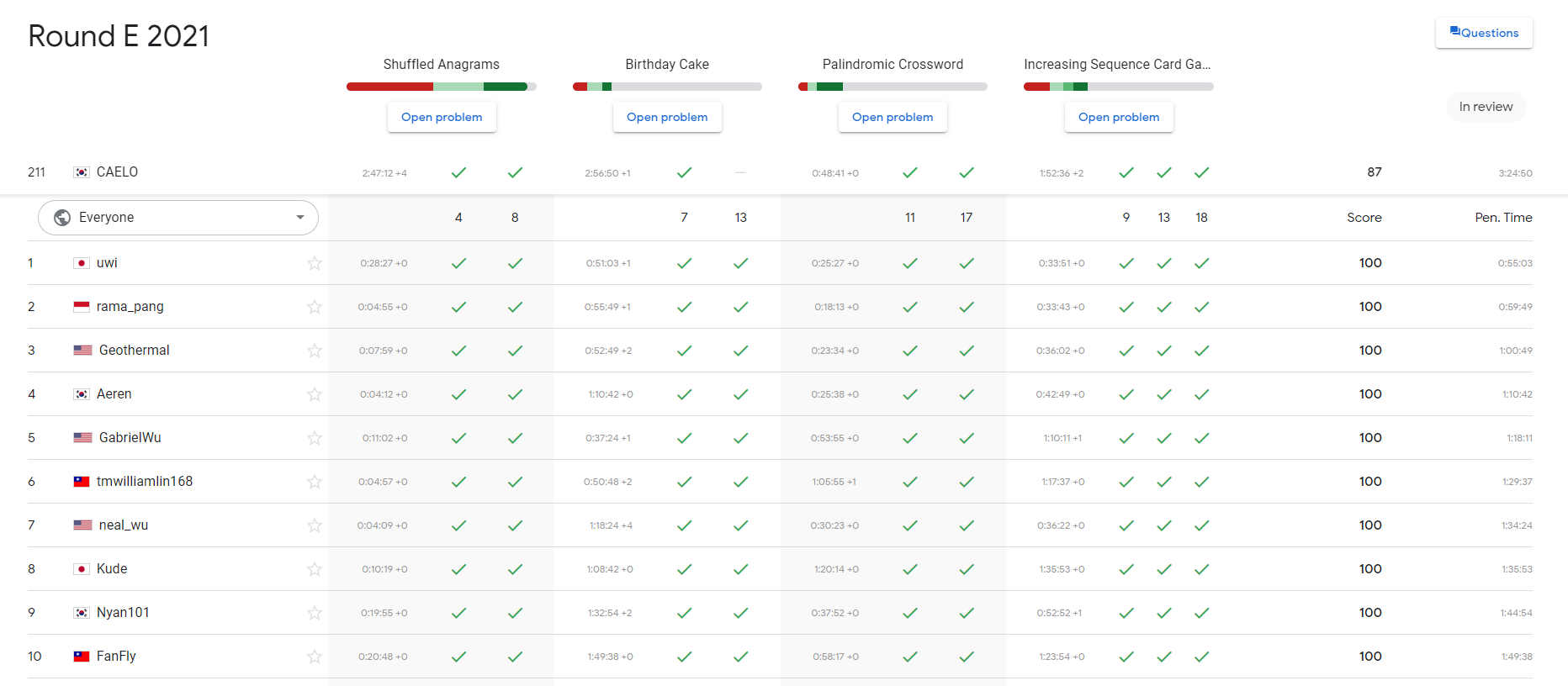
결과는 87점 / 전체 211등 / 한국 7등으로 지금까지 본 것들 중 제일 좋은 성적이었다.
한 테스트셋만 더 맞췄으면 100점인 것이 조금 아쉽다.
Shuffled Anagrams
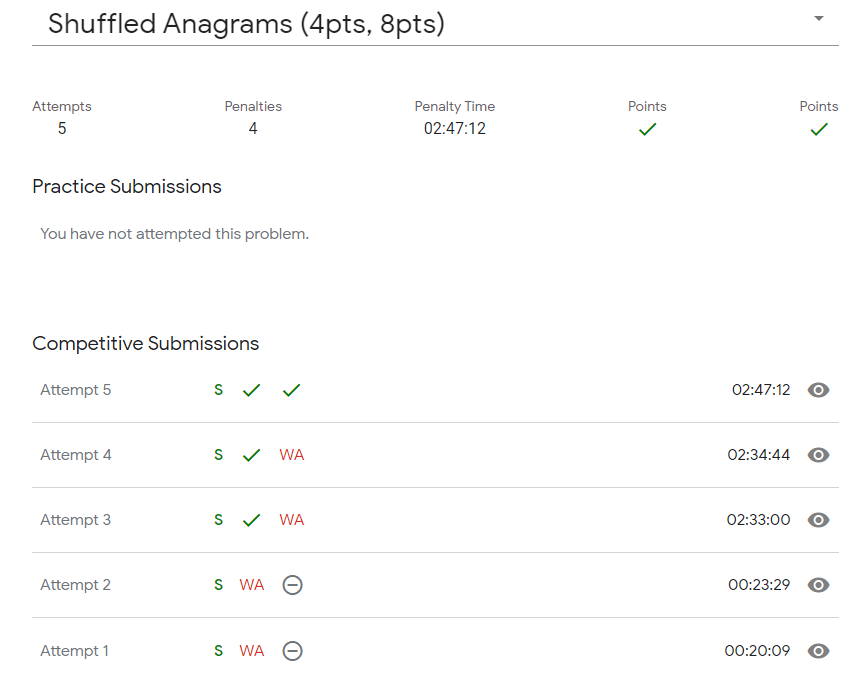
올해 치러진 라운드들의 첫 문제 중 정답자가 제일 적었다.
나도 초반에 풀다가 안돼서, 마지막에 다시 풀기 시작했고 결국 13분을 남기고 패스를 했다.
주어진 문자열을 재배치해 모든 자리의 문자들이 기존 문자와 다른게 바꿀 수 있으면 그중 아무거나 출력하고, 없다면 IMPOSSIBLE을 출력한다.
우선 IMPOSSIBLE인지 아닌지를 판단하는 것이 우선이었다.
naive하게 생각했을 때 전체 길이의 절반을 넘는 개수의 문자가 있으면 불가능할 것 같았다.
그런 문자가 없을 때 가능하단 것을 증명하기 막막했는데, 문자의 종류가 세 개일 때를 생각해 보다가 영감이 떠올랐다.
만약 a가 x개, b가 y개, c가 z개 있다면 (WLOG, $ x \ge y \ge z $) $ y + z \ge x $를 만족해야 shuffled anagram을 만들 수 있다.
이는 변의 길이가 x, y, z인 삼각형의 성립 조건과 유사하다.
그래서 기하적으로 접근하다 보니, 솔루션을 찾게 되었다.
주어진 문자열 내 문자가 각각 $ x_1 \ge x_2 \ge … \ge x_n $개 존재하면, 각 변의 길이가 $ x_1, x_2, …, x_n $인 n각형을 만든다.
그리고 각 변 위에, 해당 문자가 일정한 간격으로 놓여있다고 상상해보자.
모든 문자를 한 쪽 방향으로 $ x_1 $만큼 옮기면, 각 문자가 놓여있는 변은 원래 놓여있던 변과 다르게 된다.
즉, 원래 문자열에서 각 문자를 현재 놓여있는 변이 나타내는 문자로 치환해 주면 된다.
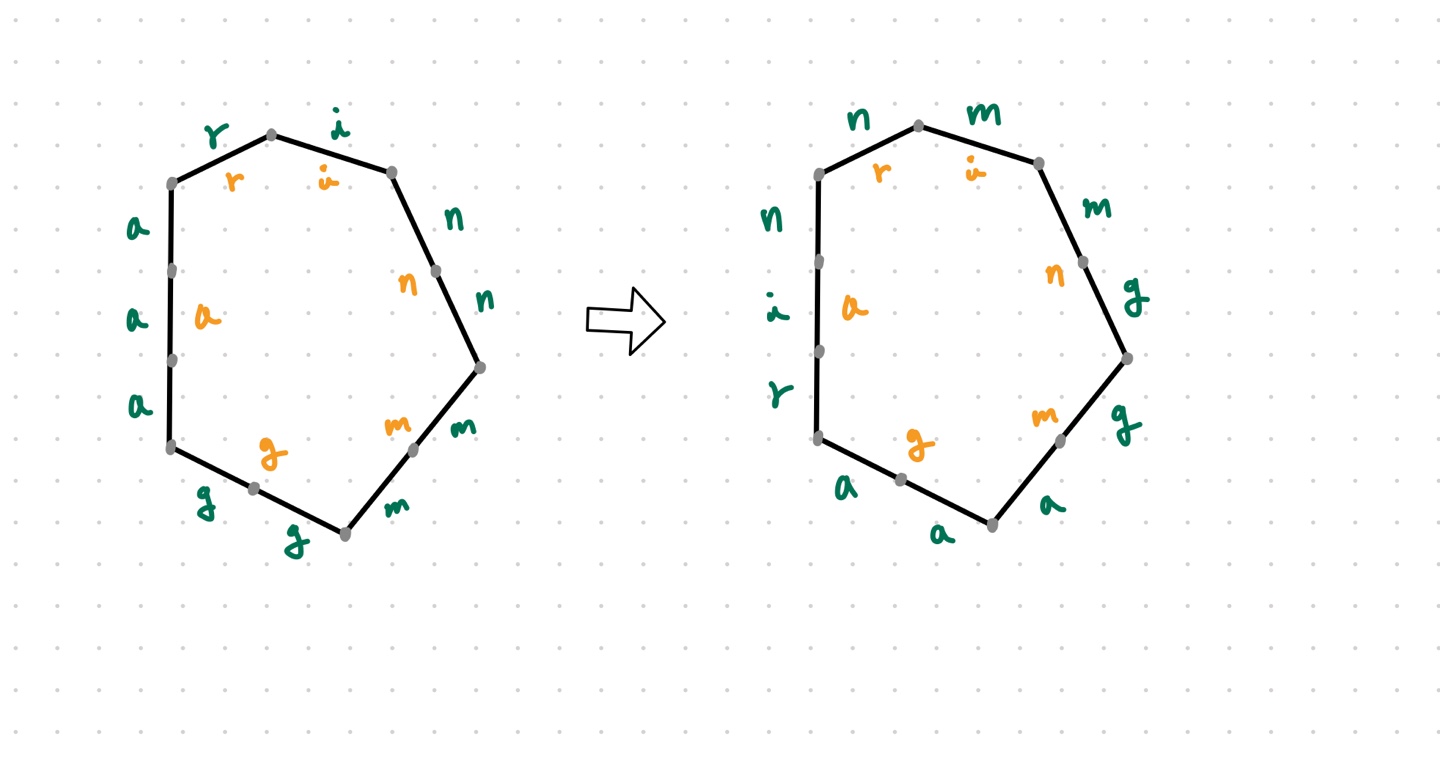
설명이 장황했는데, ‘anagramming’으로 예시를 들어보겠다.
일단 이 문자열엔 a가 3번, g가 2번, m이 2번, n이 2번, i가 1번, r이 1번 등장한다.
이를 토대로 다각형을 만들면 왼쪽처럼 육각형이 되고, 제일 긴 변의 길이인 3만큼 시계 반대 방향으로 옮기면 오른쪽처럼 된다.
오른쪽 그림을 보고, a 2개는 g로, 1개는 m으로, g 1개는 m으로, 1개는 n으로, … 이런 식으로 변환시켜주면 된다.
import sys
from copy import deepcopy
from collections import defaultdict
for t in range(int(sys.stdin.readline())):
word = sys.stdin.readline().strip()
res = [0] * len(word)
counter = defaultdict(int)
for i in range(len(word)):
counter[word[i]] += 1
counter = sorted(map(list, counter.items()), key=lambda x: -x[1])
if 2 * counter[0][1] > len(word):
print(f'Case #{t + 1}: IMPOSSIBLE')
continue
remain = deepcopy(counter)
change = [[0] * 26 for _ in range(26)]
idx = 1
for char1, num1 in counter:
while True:
char2, num2 = remain[idx % len(remain)]
if num2 == 0:
idx += 1
continue
if num1 <= num2:
change[ord(char1) - 97][ord(char2) - 97] += num1
remain[idx % len(remain)][1] -= num1
break
else:
change[ord(char1) - 97][ord(char2) - 97] += num2
remain[idx % len(remain)][1] -= num2
num1 -= num2
idx += 1
res = [0] * len(word)
for i in range(len(word)):
char1 = ord(word[i]) - 97
for j in range(26):
if change[char1][j]:
change[char1][j] -= 1
res[i] = chr(j + 97)
break
print(f'Case #{t + 1}: {"".join(res)}')
Birthday Cake
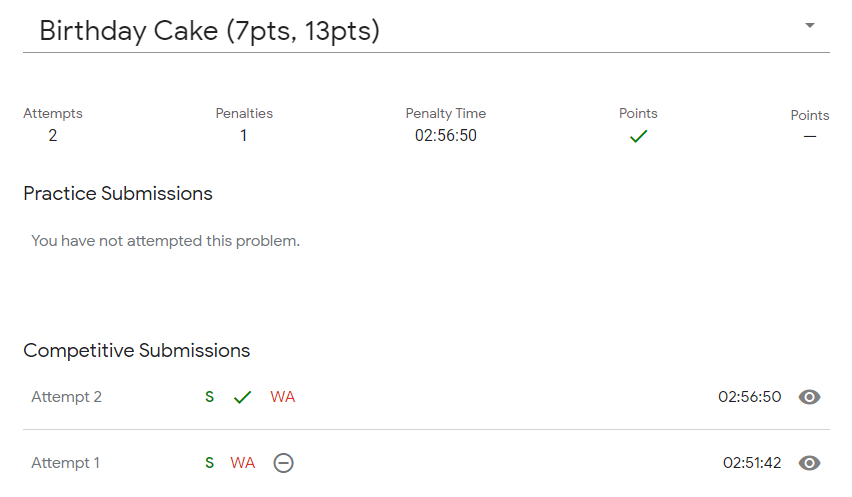
시간이 없어서 급하게 테스트셋1에 대해서만 풀었다.
K가 1로 제한돼 있어 쉽게 풀 수 있었다.
테스트셋2의 해설을 보니, 정말 내가 싫어하는 스타일의 문제다.
다양한 코너 케이스가 존재하고 엄밀히 증명하기엔 또 까다로운, 정답률이 제일 낮을만한 문제였다.
심지어 테스트 데이터를 다운 받아 디버깅을 했다.
고로 통과 코드만 첨부하고 별다른 코멘트를 남기지 않겠다.
import sys
from math import ceil
for t in range(int(sys.stdin.readline())):
r, c, k = map(int, sys.stdin.readline().split())
r1, c1, r2, c2 = map(int, sys.stdin.readline().split())
n = ceil((r2 - r1 + 1) / k)
m = ceil((c2 - c1 + 1) / k)
ans1 = n + m - m * ((r1 == 1) + (r2 == r))
ans2 = ans1
if (c1 != 1) and (c2 != c):
ans1 += ceil((r - r1 + 1) / k) + m
elif (c1 == 1) and (c2 == c):
ans1 += m - n
else:
ans1 += m
if (c1 != 1) and (c2 != c):
ans2 += ceil(r2 / k) + m
elif (c1 == 1) and (c2 == c):
ans2 += m - n
else:
ans2 += m
ans3 = n + m - n * ((c1 == 1) + (c2 == c))
ans4 = ans3
if (r1 != 1) and (r2 != r):
ans3 += ceil((c - c1 + 1) / k) + n
elif (r1 == 1) and (r2 == r):
ans3 += n - m
else:
ans3 += n
if (r1 != 1) and (r2 != r):
ans4 += ceil(c2 / k) + n
elif (r1 == 1) and (r2 == r):
ans4 += n - m
else:
ans4 += n
ans = min(ans1, ans2, ans3, ans4)
ans += (r2 - r1 + 1) * (c2 - c1 + 1) - 1 + int((r2 - r1) / k) * int((c2 - c1) / k)
print(f'Case #{t + 1}: {ans}')
Palindromic Crossword
체감상 이 문제가 제일 쉬웠던 것 같다.
정답이 항상 팰린드롬인 크로스워드 배열이 주어지면, 채울 수 있는 칸을 모두 채워야 한다.
한 지점에 정답이 채워져 있으면, 가로로 몇 칸짜리 단어인지, 세로로 몇 칸짜리 단어인지 세어본다.
그 후 대칭되는 지점에 똑같은 문자를 채워 넣으면 된다.
우선 전체를 훑으며 정답이 채워진 칸의 좌표를 큐에 저장한다.
그리고 큐에 있는 각 좌표쌍에 대해, #이 나오거나 range를 벗어날 때까지 좌우로, 상하로 탐색한다.
만약 (x, y)에서 왼쪽으로 a칸, 오른쪽으로 b칸이 있다면 이 가로 단어의 가운데를 기준으로 (x, y)의 대칭점의 좌표는 (x, y + b - a)이다.
이 대칭점이 빈 칸이라면 정답을 채워 넣고 큐에 새로운 좌표를 넣는다.
import sys
for t in range(int(sys.stdin.readline())):
n, m = map(int, sys.stdin.readline().split())
board = [list(sys.stdin.readline().strip()) for _ in range(n)]
queue = []
for i in range(n):
for j in range(m):
if board[i][j].isalpha():
queue.append((i, j))
ans = 0
while queue:
x, y = queue.pop()
for j in range(y + 1):
if board[x][y - j] == '#':
left = j - 1
break
else:
left = j
for j in range(m - y):
if board[x][y + j] == '#':
right = j - 1
break
else:
right = j
for i in range(x + 1):
if board[x - i][y] == '#':
up = i - 1
break
else:
up = i
for i in range(n - x):
if board[x + i][y] == '#':
down = i - 1
break
else:
down = i
if board[x][y + right - left] == '.':
board[x][y + right - left] = board[x][y]
queue.append((x, y + right - left))
ans += 1
if board[x + down - up][y] == '.':
board[x + down - up][y] = board[x][y]
queue.append((x + down - up, y))
ans += 1
print(f'Case #{t + 1}: {ans}')
for row in board:
print(''.join(row))
Increasing Sequence Card Game
사실 테스트셋 별로 다른 문제를 푼 느낌이다.
엄청 신기하고 재밌고 잘 만든 문제이다.
문제를 요약하자면, 1부터 N으로 이뤄진 수열이 주어졌을 때 초항을 포함한 LIS 길이의 기댓값을 구하는 것이다.
N이 4 이하일 때 모든 경우를 계산해보았다.
| N | 2 | 3 | 4 |
|---|---|---|---|
| 1 | 1 | 2 | 6 |
| 2 | 1 | 3 | 11 |
| 3 | - | 1 | 6 |
| 4 | - | - | 1 |
예로 들어 3번 행, 4번 열은 N이 4일 때 초항을 포함한 LIS 길이가 3인 수열이 6개 있다는 뜻이다.
규칙을 찾기 생각보다 어려웠다.
테스트셋3의 N 범위가 10 ** 18이라, DP로 접근해도 TLE가 날 것 같았다.
그런데 4번째 열의 6, 11, 6, 1… 뭔가 익숙하지 않은가?
1 + 2 + 3 = 6
1 * 2 + 2 * 3 + 3 * 1 = 11
1 * 2 * 3 = 6
그렇다. $ (x + 1)(x + 2)(x + 3) = x^3 + 6x^2 + 11x + 6 $이다.
왜 이렇게 되는진 일단 문제를 풀고 나서 생각해 보자.
기댓값을 구하는 식은 N = 4를 예로 들면 다음과 같다.
\[\frac{1 \times 6 + 2 \times 11 + 3 \times 6 + 4 \times 1}{4!}\]즉 위 다항식에서 계수와 차수가 곱해져야 한다.
그러려면 양변의 x를 곱한 후 미분하면 된다.
\[x(x + 1)(x + 2)(x + 3) = x^4 + 6x^3 + 11x^2 + 6x\] \[(x + 1)(x + 2)(x + 3) + x(x + 2)(x + 3) + x(x + 1)(x + 3) + x(x + 1)(x + 2) = 4x^3 + 3 \times 6x^2 + 2 \times 11x + 6\]이제 양변에 1을 대입하고 $ 4! $로 나누면 우변은 기댓값이 된다.
\[\frac{2 \times 3 \times 4 + 1 \times 3 \times 4 + 1 \times 2 \times 4 + 1 \times 2 \times 3}{4!} = \frac{4 + 3 \times 6 + 2 \times 11 + 6}{4!}\]좌변을 정리하면 다음처럼 된다.
\[\frac{2 \times 3 \times 4 + 1 \times 3 \times 4 + 1 \times 2 \times 4 + 1 \times 2 \times 3}{4!} = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}\]놀랍지 않은가?
구하고자 했던 기댓값은 1부터 N까지 역수의 합이었다.
그러므로 정답을 O(N)만에 구할 수 있다.
이 풀이는 테스트셋2까지는 유효하지만, 테스트셋3은 TLE가 뜬다.
하지만 어렵지 않게, $ y = \frac{1}{x} $의 적분값과 연관 지어 생각해 볼 수 있다.
$ \sum_{x = 1}^{n}\frac{1}{x} $는 $ 1 + \int_{1}^{n} \frac{1}{x}dx $보다 살짝 작다.
이 두 값의 차를 오일러-마스케로니 상수 (Euler-Mascheroni constant)라고 하며 다음과 같이 정의된다.
\[\gamma = \lim_{n \rightarrow \infty} (\sum_{k = 1}^n \frac{1}{k} - \ln n) = \int_{1}^{\infty} (\frac{1}{\lfloor x \rfloor} - \frac{1}{x})dx = 0.5772156649...\]실제 정답과의 오차가 $ 10^{-6} $보다 작기만 하면 되므로, 이 상수와 적분 값을 이용해 정답에 근사시킬 수 있다.
그렇다면 왜 위와 같은 결과가 나왔을까?
N = 5이고 LIS의 길이가 2일 때를 생각해 보자.
이때의 경우의 수는 $ 1 \times 2 \times 3 + 2 \times 3 \times 4 + 3 \times 4 \times 1 + 4 \times 1 \times 2 = 50 $이다.
우선 LIS가 될 수 있는 경우는 (1, 5), (2, 5), (3, 5), (4, 5)로 다섯 가지이다.
미리 말하자면 위 계산식의 각 항은 각 LIS 경우에 나머지 수들을 끼워 넣는 경우의 수이다.
무슨 말이냐면, LIS가 (3, 5)일 때, 4는 무조건 5 뒤에 있어야 되고, 1과 2는 3 뒤에만 있으면 된다.
고로 $ 1 \times 3 \times 4 = 12 $가지 경우의 수가 발생한다.
rough하게 생각해보면 LIS의 길이가 k일 때, 남은 n - k개의 수들을 끼워 넣어야 하고, 모든 경우의 수열을 고려하므로 위와 같은 식이 나오는 것이다.
물론 엄밀하진 않았지만, 어떤 맥락인지는 파악이 돼서 더 깊이 들어가진 않겠다.
import sys
from math import log
for t in range(int(sys.stdin.readline())):
n = int(sys.stdin.readline())
if n > 10 ** 6:
print(f'Case #{t + 1}: {log(n + 1) + 0.5772156649}')
else:
ans = 0
for i in range(1, n + 1):
ans += 1 / i
print(f'Case #{t + 1}: {ans}')


Leave a comment